§1.9
函数的连续性与间断点
一、函数的连续性
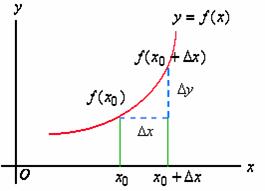
1、增量
设变量![]() 从它的初值
从它的初值![]() 变到终值
变到终值![]() ,终值
,终值![]() 与初值
与初值![]() 的差
的差 ![]() ,称为变量
,称为变量![]() 的增量,记为
的增量,记为![]() ,即:
,即:![]() 。
。
注意:
(1)、增量![]() 可正亦可负(不要由于名称中的“增”字,而认为
可正亦可负(不要由于名称中的“增”字,而认为![]() )。
)。
(2)、![]() 应视为一个整体记号。
应视为一个整体记号。
假设函数![]() 在点
在点![]() 的某一个邻域内有定义,当自变量
的某一个邻域内有定义,当自变量![]() 在邻域内从
在邻域内从![]() 变到
变到![]() 时, 函数
时, 函数![]() 相应的从
相应的从![]() 变到
变到![]() , 我们将差值
, 我们将差值
![]()
称之为函数![]() 在点
在点![]() 处的增量。
处的增量。
函数增量的几何意义如下:
2、函数的连续性
所谓函数在点![]() 处连续是指:
处连续是指:
![]()
或 ![]()
其严格定义如下:
【定义1】
设![]() 在点
在点![]() 的某一邻域内有定义,如果当自变量增量
的某一邻域内有定义,如果当自变量增量![]() 趋向于零时, 对应的函数增量
趋向于零时, 对应的函数增量![]() 也趋向于零, 则称函数
也趋向于零, 则称函数![]() 在点
在点![]() 处连续。
处连续。
令
![]() ,则
,则 ![]()
![]()
可见:(1)式等价于 ![]()
因此,函数的连续性定义可以改成下述新的形式。
【定义2】
设![]() 在点
在点![]() 的某一邻域内有定义, 如果函数
的某一邻域内有定义, 如果函数![]() 当
当![]() 时的极限存在且等于它在该点的函数值, 即
时的极限存在且等于它在该点的函数值, 即
![]()
则称函数![]() 在点
在点![]() 处连续。
处连续。
关于函数的连续性,还有几个相应的概念。
1、如果![]() ,称函数
,称函数![]() 在
在![]() 处左连续。
处左连续。
2、如果![]() ,称函数
,称函数![]() 在
在![]() 处右连续。
处右连续。
3、如果函数在区间![]() 上每一点均连续, 称函数在区间
上每一点均连续, 称函数在区间![]() 上连续;
上连续;
若![]() 包括端点,那么函数在右端点的连续性是指左连续,而在左端点的连续性是指右连续。
包括端点,那么函数在右端点的连续性是指左连续,而在左端点的连续性是指右连续。

连续函数的图象是一条连绵不间断的曲线。这是因为,如果函数的图象上出现了“空洞”、“断裂”,那么函数在该点处一定不连续。请看示例图。
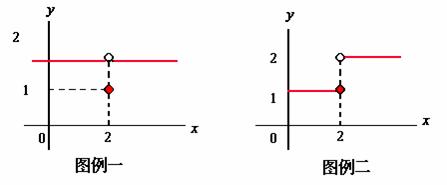
在![]() 处,图例一的
处,图例一的![]() , 显然,
, 显然, ![]() , 函数在
, 函数在![]() 处间断,曲线上的一个空洞。
处间断,曲线上的一个空洞。
在![]() 处,图例二的增量为
处,图例二的增量为
![]()
显然,![]() 。曲线在
。曲线在![]() 处有一段阶梯。
处有一段阶梯。
3、证明函数极限的方法
证明函数![]() 在点
在点![]() 连续,等价于证明下述极限
连续,等价于证明下述极限
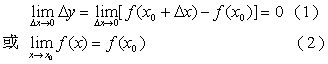
若要证明函数![]() 在区间
在区间![]() 上连续,只需对
上连续,只需对![]() 上任意一点
上任意一点![]() 证明(1)或(2)成立。
证明(1)或(2)成立。
在§6(极限运算法则)中,我们业已证明了结论:
(1)、如果![]() 是多项式函数,
是多项式函数, ![]() 有
有 ![]() ,这表明多项式函数
,这表明多项式函数![]() 在
在 ![]() 内连续;
内连续;
(2)、如果![]() 是有理分式函数,
是有理分式函数, ![]() ,只要
,只要 ![]() ,有
,有![]() , 这表明有理分式函数
, 这表明有理分式函数![]() 在其定义域内连续。
在其定义域内连续。
【例1】证明函数![]() 在
在 ![]() 内连续。
内连续。
证明:
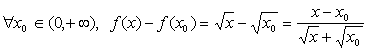
则有 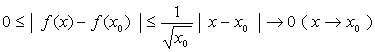
故有 ![]() ,据函数在点
,据函数在点![]() 连续的定义
连续的定义![]() 在
在![]() 连续,又由于
连续,又由于![]() 是
是![]() 上的任意一点,因此,函数在区间
上的任意一点,因此,函数在区间![]() 上连续。
上连续。
【例2】证明函数![]() 在
在![]() 上连续。
上连续。
证明:
![]() ,当
,当![]() 有增量
有增量![]() 时,对应的函数增量为
时,对应的函数增量为
![]()
因 ![]()
故 ![]()
据两边夹法则,当![]() 时,
时,![]() ,进而
,进而![]() ,
,
这便证明了函数![]() 对于任何
对于任何![]() 是连续的,继而证明了函数在区间
是连续的,继而证明了函数在区间![]() 上的连续性。
上的连续性。
类似地,同学们可以仿此方法证明![]() 在
在![]() 上的连续性。
上的连续性。
二、函数的间断点
1、间断点的定义
所谓函数![]() 在
在![]() 处间断,粗略地讲,意指函数
处间断,粗略地讲,意指函数![]() 在
在![]() 处不连续。
处不连续。
那么函数在一点不连续的“正面涵义”又是什么呢? 我们仅需要将函数![]() 在
在![]() 处连续的定义中的各个条款一一地加以否定即可。
处连续的定义中的各个条款一一地加以否定即可。
设![]() 在
在![]() 的某个邻域内有定义,但
的某个邻域内有定义,但![]() 除外(即:函数
除外(即:函数![]() 在
在![]() 处可以有定义,也可以无定义),如果
处可以有定义,也可以无定义),如果![]() 有下列三种情形中之一:
有下列三种情形中之一:
(1)、在![]() 处没有定义;
处没有定义;
(2)、虽在![]() 有定义, 但
有定义, 但![]() 不存在;
不存在;
(3)、虽在![]() 有定义, 且
有定义, 且![]() 存在,但
存在,但 ![]()
则称![]() 在
在![]() 处不连续,点
处不连续,点![]() 是函数
是函数![]() 的间断点。
的间断点。
2、典型实例
【例3】![]() 在
在![]() 间断,它是振荡间断点。
间断,它是振荡间断点。
运行程序gs0106.m,可作出此函数在[-1,1]上的图象。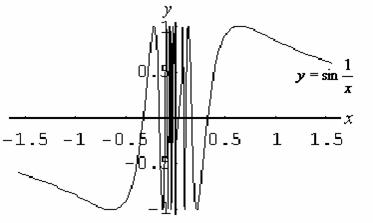
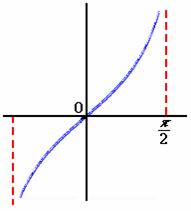
【例4】![]() 在
在![]() 间断,它是无穷间断点。
间断,它是无穷间断点。
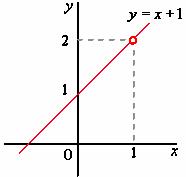
【例5】![]() 在
在![]() 间断,它是可去间断点。
间断,它是可去间断点。
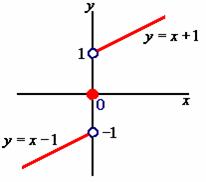
【例6】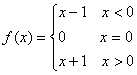 在
在![]() 间断,它是跳跃间断点。
间断,它是跳跃间断点。
3、间断点的分类
以函数的左极限![]() 、右极限
、右极限![]() 是否均存在, 将间断点分为两类。
是否均存在, 将间断点分为两类。
设![]() 是函数
是函数![]() 的间断点,若
的间断点,若
(1)、![]() 均存在,则称
均存在,则称![]() 为函数
为函数![]() 的第一类间断点;
的第一类间断点;
(2)、![]() 中至少有一个不存在,则称
中至少有一个不存在,则称![]() 为函数
为函数![]() 的第二类间断点。
的第二类间断点。
